- Introduction
- Description of algorithm (pdf) and software (zip)
- References
- Analysis of the time series
Fractal analysis is a convenient tool for study of self-similar properties of natural object. Fractal dimension characterise scaling properties of the object. Concerning application to time series, fractal analysis provide information about the degree of chaos and order in the time series being analysed. There are several methods of calculation of fractal dimension of time series (see [1], [2], [3]). The most stable estimation of fractal dimension is given by Higuchi method ([2], [3]).
Description of Higuchi method can be downloaded as pdf file. Software modules with the description can be downloaded as zip file.
[1] Feder, J. (1988) Fractals., Plenum Press, New York.
[2] Higuchi, T (1988) Approach to an Irregular Time Series on the Basis of Fractal Theory, Physica D, 31, pp. 277-283
[2] Higuchi, T (1990) Relationship between the Fractal Dimension and the Power-low Index for a Time Series: a Numerical Investigation., Physica D, 46, pp. 254-264
Analysis of the air temperature time series
Here one can see the examples of calculation of fractal dimension of the air temperature time series:
The Figure below show variations of mean annual air temperature on the station BJORNOVA (latitude 74.31°N; longitude 19.01°E)
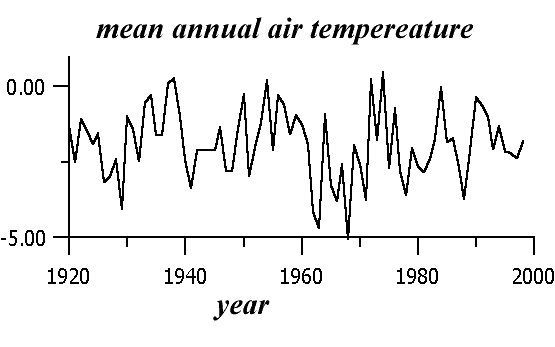
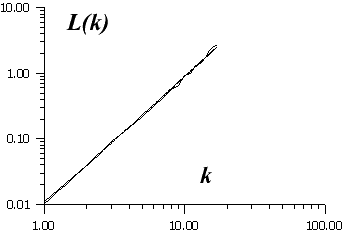
The calculation of fractal dimension D by Higuchi method give the value of D=1.94. The log-log plot below show that the error in estimation of D is rather low.
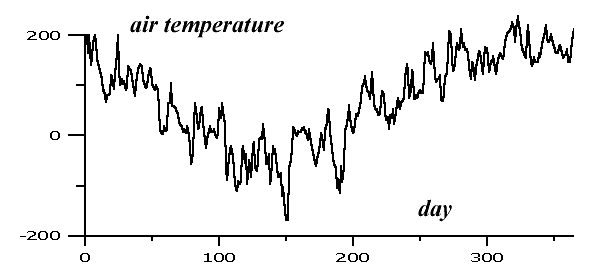
The figure below show daily air temperature variations on the station Brest (1995 year) (52.1° N 23.7° E).
The results of calculations for the station Brest for each year are shown on figure below.
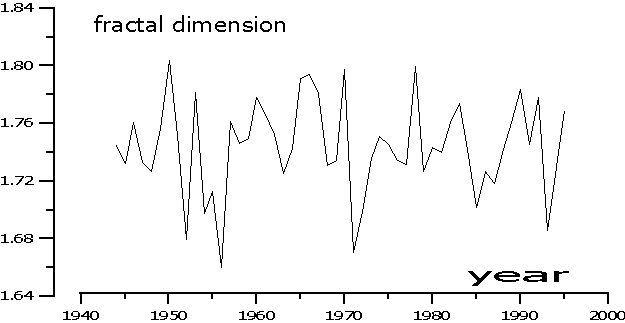
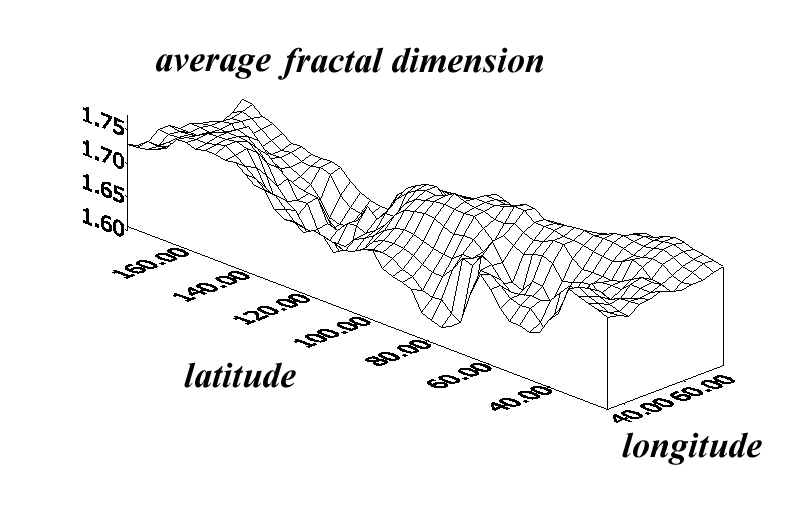
The fractal analysis of air temperature time series was performed for 223 Russian stations (Data of Russian meteorogical agency). The minimal, maximal and average values of fractal dimension were calculalated for daily air temperature time series of each year. In order to characterize the areal distribution of fractal characteristic of air temperature time series, the distribution of average value of fractal dimension over geographical coordinates was shown on figure below.